
|
우리나라 속담에 쉽게 마무리 할 수 있었던 일을 나중에 어렵게 처리한다는 뜻의 ‘호미로 막을 일을 가래로 막는다.’라는 말이 있다. 호미는 요즘에도 많이 사용하고 있기 때문에 어떻게 생겼고 어디에 사용되는 농기구인지는 잘 알고 있을 것이다. 하지만 가래가 어떤 농기구인지 모르는 사람도 있다. | |
호미로 막을 일을 ‘가래’로 막는다

|
가래는 삽처럼 생긴 가랫날의 양 귀퉁이에 끈을 묶어서 두 사람이 양쪽에서 잡아당기고, 또 다른 한 사람은 가래손잡이를 붙들고 힘과 방향을 조절하는 농기구이다. 가래를 사용하면 땅을 깊게 파거나 흙을 멀리 던져 보내는 힘든 일도 쉽게 할 수 있다. 쇠가 귀하던 옛날의 가래는 나무판을 깎아서 테두리에만 쇠를 끼워 가래의 쇠 날이 무뎌지면 대장간에서 갈아 끼웠지만, 근래의 가래는 삽과 같이 손잡이를 제외하고는 모두 쇠로 제작된다.
가래를 사용하면 적은 힘을 하나로 합쳐서 큰 힘을 만들 수 있는데, 가래와 같이 작은 힘을 합하여 큰 힘을 만드는 또 다른 기구로 두레가 있다. 두레하면 농촌에서 농사일을 공동으로 하기 위하여 마을이나 부락 단위로 둔 조직을 말하지만 여기서 말하는 두레는 낮은 곳에서 높은 곳으로 물을 퍼 올리는 농기구이다. 가래와 마찬가지로 두레도 바가지에 끈을 묶어서 두 사람이 양쪽에서 잡아당겨서 물을 퍼 올린다. 가래와 두레는 양쪽에서 힘을 가하지만 힘을 주는 방향과 이것들이 실제로 움직이는 방향은 일치하지 않는다. 이와 같은 상황을 벡터를 사용하여 수학적으로 정확히 표현할 수 있는데, 먼저 벡터에 관하여 알아본 후에 가래로 일을 할 경우를 벡터로 나타내 보자. | |
|
|

전통 농기구 가래 <사진 제공: 농업박물관> | |
|
벡터와 스칼라

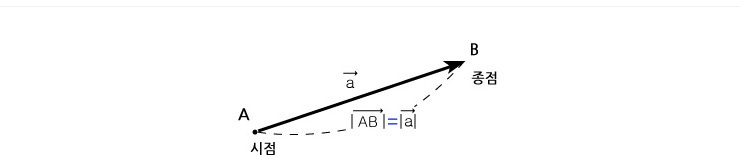
선분의 길이, 도형의 넓이나 부피, 온도 등과 같은 양은 하나의 실수로 나타낼 수 있다. 그러나 속도, 가속도, 힘 등의 양은 크기는 물론 방향도 가지고 있으므로 크기와 방향이 모두 정해져야만 그 양을 나타낼 수 있다. 일반적으로 크기만을 갖는 양을 스칼라(scalar)라 하고 크기와 동시에 방향을 갖는 양을 벡터(vector)라고 한다. | |
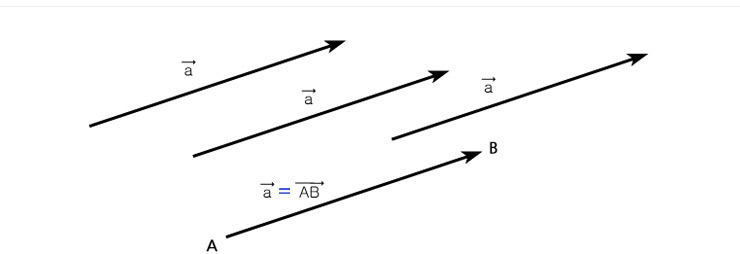
한 벡터를 평행이동하여 얻은 벡터는 모두 같은 것으로 여긴다.

|
한편 벡터 가운데에서 특정한 크기를 갖는 벡터가 있는데, 크기가 1인 단위벡터와 크기가 0인 벡터를 영벡터가 있다. 단위벡터는 보통 기호 u로 나타내고, 영벡터는 기호 0와 같이 나타낸다. 벡터는 크기와 방향이 있다고 했으므로 크기가 0인 영벡터도 방향을 가지고 있어야 하기 때문에 영벡터의 방향은 임의로 생각한다. 즉, 어떤 방향도 다 될 수 있는 것으로 생각한다.
벡터를 더하는 법

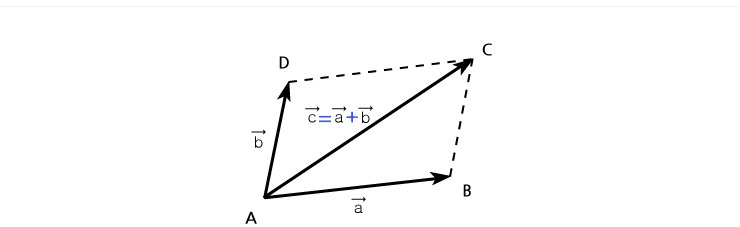
벡터는 평면에서뿐만 아니라 공간에서도 생각할 수 있는데, 평면에서의 벡터를 평면벡터, 공간에서의 벡터를 공간벡터라고 한다. 평면이나 공간에 있는 두 벡터는 서로 합할 수 있는데, 두 벡터 a, b 대하여 a 를 평면이나 공간에 있는 두 벡터는 서로 합할 수 있는데, 두 벡터 a, b 대하여 a 를  , b를 , b를  로 나타낼 때, 그림과 같이 평행사변형 ABCD를 그리면 다음을 알 수 있다. 로 나타낼 때, 그림과 같이 평행사변형 ABCD를 그리면 다음을 알 수 있다. | |
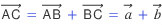
따라서 벡터 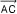 는 두 벡터의 합 c = a + b 나타낸다. 는 두 벡터의 합 c = a + b 나타낸다. | |
|
벡터의 덧셈은 위와 같이 벡터를 화살표로 표시하면 간단히 나타낼 수 있지만 벡터의 덧셈 법칙은 스칼라 양에 대한 법칙과는 같지 않다. 예를 들면 오른쪽 그림에서 벡터 a 의 크기가 3이고 벡터 b의 크기가 2라면, 그림에서와 같이 두 벡터를 더한 결과인 벡터 c = a + b의 크기는 5가 아니고 5보다 더 작다. 즉, 다음의 관계가 성립한다. | |
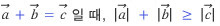

|
그리고 이 크기는 벡터 a의 방향과 벡터 b의 방향이 상대적으로 어떤 관계에 있느냐에 따라 달라진다. 벡터의 덧셈을 알았으므로 앞에서 소개했던 가래의 경우를 벡터로 표시해 보자. 가래는 두 사람이 양쪽에서 잡아당기고 또 다른 한 사람은 가래손잡이를 붙들고 힘과 방향을 조절하므로 3개의 벡터로 나타내야 한다. 이때 양쪽에서 잡아당기는 힘을 각각 벡터 a, b 손잡이에 주는 힘을 벡터 c 라고 하자. 이 세 벡터의 합을 구하면 가래의 힘인 벡터 f가 나온다. | |

가래는 세 사람의 힘을 합쳐 큰 힘을 낼 수 있다.
|
벡터의 연구는 16세기부터

벡터는 16세기 네덜란드의 수학자 스테빈(S. Stevin, 1548~1620)에 의하여 힘의 삼각형에 대한 문제가 제기되면서 등장하였다. 그러나 벡터에 관한 이론은 뉴턴의 역학의 연구에서 출발하였다고 볼 수 있으며 19세기에 들어와 수학자이며 물리학자인 영국의 해밀턴(W. R. Hamilton, 1805~1865), 미국의 깁스(J. W. Gibbs, 1839~1903) 등이 벡터를 수학적으로 다루기 시작했다. 특히 그라스만(H. G. Grassman, 1809~1877)은 벡터를 차원 공간의 기하학으로 설명하였으며 벡터의 내적과 외적을 정의하였다. 수학에서 벡터를 다루는 분야를 벡터해석학이라고 하는데, 벡터해석학에서 가장 중요한 내용은 벡터의 내적과 외적이다. 앞으로 벡터에 대해서 좀 더 알아보도록 하자. |
Source : http://navercast.naver.com/contents.nhn?contents_id=4554 |




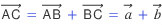

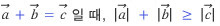




 하나의 실수로 나타낼 수 없다. 따라서 벡터는 오른쪽 그림과 같이 크기를 나타내는 선분 AB에 방향을 나타내는 화살표를 붙여 표현한다.
하나의 실수로 나타낼 수 없다. 따라서 벡터는 오른쪽 그림과 같이 크기를 나타내는 선분 AB에 방향을 나타내는 화살표를 붙여 표현한다. ,
, 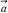 또는 굵은 글자체 a로 나타내고, 점 A를 벡터
또는 굵은 글자체 a로 나타내고, 점 A를 벡터 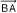 이다. 즉, 다음이 성립한다.
이다. 즉, 다음이 성립한다. 로 나타낼 때, 그림과 같이 평행사변형 ABCD를 그리면 다음을 알 수 있다.
로 나타낼 때, 그림과 같이 평행사변형 ABCD를 그리면 다음을 알 수 있다.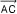 는 두 벡터의 합 c = a + b 나타낸다.
는 두 벡터의 합 c = a + b 나타낸다.